The Geometry of the Infinite

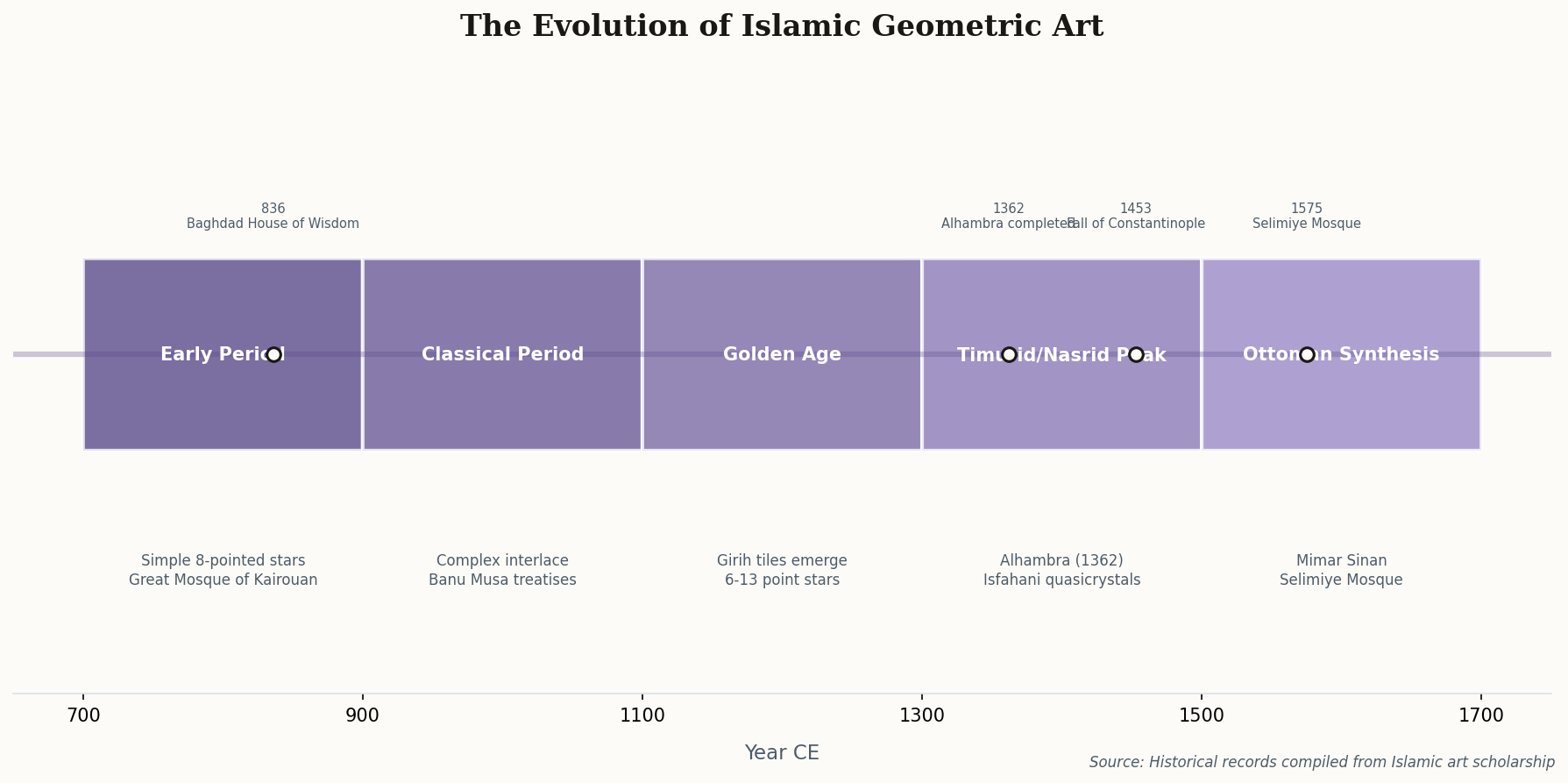
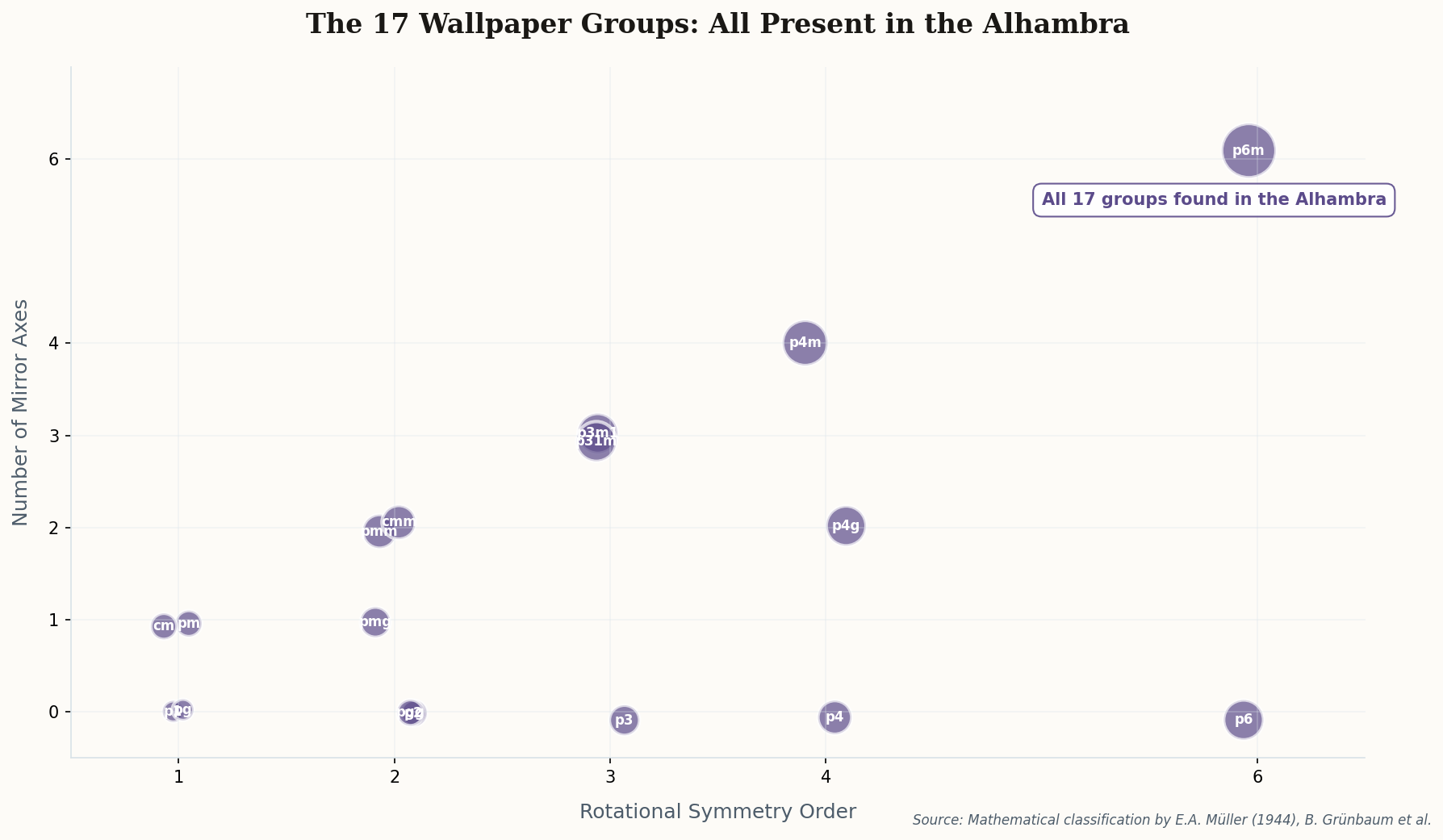
In 1944, mathematician Edith Müller sat down with photographs of the Alhambra in Granada, Spain, and made a startling claim: this 14th-century palace contained examples of all 17 possible ways to tile a plane with repeating patterns. Every wallpaper group. Every symmetry operation. All of them, created six centuries before mathematicians had even proven that exactly 17 such groups exist.

The mathematics here isn't decorative—it's fundamental. A "wallpaper group" describes the symmetries of a pattern that repeats infinitely in two directions. You can rotate it, reflect it, glide it, or combine these operations in specific ways. The Russian crystallographer Evgraf Fedorov proved in 1891 that there are precisely 17 distinct combinations. The Nasrid artisans of the Alhambra found all 17 through pure visual intuition, compass, and straightedge.

Walk through the Hall of the Abencerrajes and you're walking through a textbook of mathematical group theory, rendered in ceramic and stucco. The muqarnas dome overhead—a honeycomb of interlocking cells—isn't just beautiful. It's a three-dimensional proof that these medieval craftsmen understood something profound about the structure of space itself.

In 2007, Harvard physicist Peter Lu was wandering through Uzbekistan when he noticed something impossible. The 15th-century Darb-e Imam shrine in Isfahan featured patterns with fivefold and tenfold rotational symmetry that never exactly repeated—the same "quasiperiodic" structure that mathematician Roger Penrose had discovered in the 1970s and that had won Dan Shechtman the 2011 Nobel Prize in Chemistry for finding in physical quasicrystals.

The medieval Islamic artisans had done it 500 years earlier using girih tiles—a set of just five shapes (decagon, pentagon, hexagon, bowtie, rhombus) whose edges are decorated with lines that form continuous strapwork when assembled. Lu and physicist Paul Steinhardt demonstrated that these tiles could generate infinite non-repeating patterns through a "self-similar transformation"—essentially constructing a fractal.

This wasn't just decorative genius. Before Lu's discovery, scientists believed that quasiperiodic order—filling infinite space without ever strictly repeating—was impossible in crystalline matter. The Isfahan artisans had intuited mathematical structures that 20th-century physics considered impossible. They were doing materials science avant la lettre, with clay and compass.

How did illiterate craftsmen create patterns that would stump mathematicians for centuries? The answer lies in a remarkable collaboration between scholars and artisans that flourished during the Islamic Golden Age.

In 10th-century Baghdad, the Persian mathematician Abu al-Wafa' al-Buzjani wrote a treatise called "On Those Parts of Geometry Needed by Craftsmen." It wasn't abstract theory—it was a practical manual showing artisans how to construct complex geometric figures using only compass and straightedge. The Banu Musa brothers translated Greek geometric texts and expanded on Euclidean knowledge. Omar Khayyam—yes, the poet—solved cubic equations geometrically.

This knowledge flowed directly to the guilds. As one early guild saying put it: "Whoever does not know geometry cannot be an architect." Six centuries later, Mimar Sinan, the "Grand Architect" of the Ottoman Empire, would use geometry not just for decoration but for structural integrity and acoustic perfection in masterpieces like the Selimiye Mosque.

The collaboration was formalized. Scholars provided the theory; craftsmen provided the practice. The result was a knowledge system that could transmit mathematical sophistication without requiring literacy—encoded in the patterns themselves.

Pick up any Islamic geometric pattern featuring 10-pointed stars and you'll find the golden ratio hiding in plain sight. It's not decoration—it's mathematical necessity.

The golden ratio (φ ≈ 1.618) appears naturally in the relationship between the edge lengths of pentagons and decagons. When artisans drew 10-pointed stars using compass and straightedge, they were implicitly encoding φ into every proportion. The five girih tiles—the building blocks of the most complex Islamic patterns—all contain internal angles that are multiples of 36°, the fundamental angle of the pentagon. This isn't coincidence; it's why these tiles can create quasiperiodic patterns at all.

The 8-pointed star—the most common in Islamic art—tessellates cleanly with 45° angles. Simple, versatile, satisfying. But the 10-pointed star does something stranger: it can only tile the plane non-periodically. Medieval artisans discovered through trial and error what Penrose proved mathematically: certain symmetries can fill space infinitely without ever exactly repeating. They chose these patterns deliberately, perhaps because the infinite non-repetition felt more spiritually resonant than the predictable march of periodic tiles.

The Great Mosque of Kairouan in Tunisia (670 CE) laid the first stones. The Great Mosque of Isfahan became a laboratory of Persian geometry over a thousand years. The Alcázar of Seville blended Gothic and Islamic geometry through Mudéjar craftsmen. Each monument represents a chapter in an ongoing conversation between mathematics and stone.

That conversation continues. Jean Nouvel's Louvre Abu Dhabi (2017) features a massive dome consisting of 7,850 stars arranged in a complex geometric lattice. As sunlight passes through, it creates what Nouvel calls a "rain of light"—the same effect you'd see in a traditional mashrabiya screen, scaled to monumental proportions. The Institut du Monde Arabe in Paris goes further, with motor-controlled apertures that open and close like camera shutters, mimicking traditional geometric screens while responding to light levels in real time.

Modern parametric design software—Grasshopper, Rhino—now lets designers generate Islamic patterns algorithmically, exploring variations that would have taken medieval artisans years to construct by hand. Artists like Monir Shahroudy Farmanfarmaian and Rasheed Araeen have fused these ancient patterns with contemporary minimalism, proving the tradition isn't a museum piece but a living language.

Why geometry? Why not the human figure, landscapes, the natural world?

The answer isn't just religious prohibition. Aniconism—the avoidance of figural representation in sacred contexts—created the conditions, but it doesn't explain the passion. Islamic geometric art expresses something deliberate about how these cultures understood reality itself.

The concept of tawhid—the absolute oneness of God—finds its visual analog in patterns that begin from a single point and expand infinitely outward. The pattern has no privileged center, no beginning, no end. Every point is equivalent. The infinite is made visible through finite means. As philosopher Seyyed Hossein Nasr writes: "Art is the mirror of a culture and its world view... Islamic art reflects the cultural values of Islam, and reveals the way Muslims view the spiritual realm and the universe."

The act of drawing these patterns—following the compass, watching the geometry unfold—was itself considered a form of dhikr, remembrance of the divine. The infinite regularity of the pattern mirrors the infinite regularity of divine order. The craftsman isn't decorating a mosque; he's making visible the underlying structure of creation.

This is geometry as spiritual technology. A meditation practice encoded in tile and stucco. A thousand years before fractal mathematics or chaos theory, Islamic artisans were exploring the same territory through pure visual intuition: how simple rules, endlessly applied, generate structures of incomprehensible complexity. The universe itself, perhaps, works the same way.